
Here we discuss the Methods of using Piecewise Function in Matlab with various statements and examples. If its small, you boil and mash the potato. This is a guide to Piecewise Function in Matlab. Returns a piecewise function from a list of (interval, function) pairs. As a non-math example, we could imagine cooking potatoes in different ways depending on the size of the potato. And the vectorized approach used in many applications. But, the if-else (loop) approach not used for real-time implementations. Piecewise Functions This worksheet contains a number of examples of the use of the piecewise function. As we see above there are three approaches to represent piecewise functions. Piecewise functions are mainly used to represent functions that have various input ranges with different conditions.
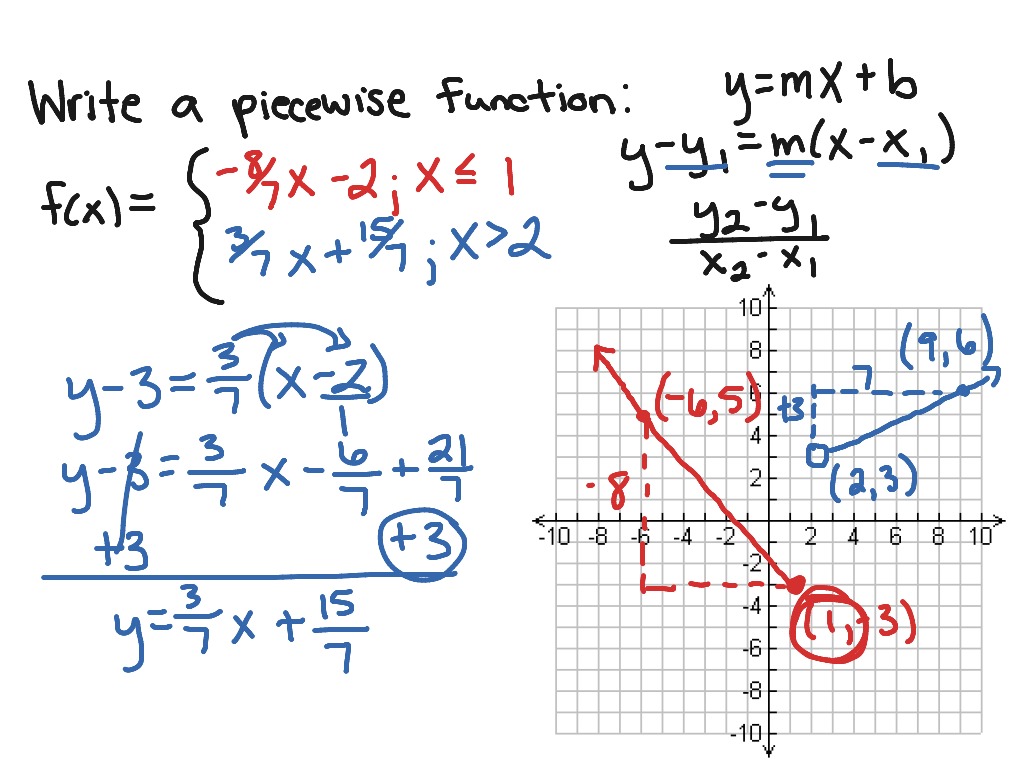
Matlab programĬonclusion – Piecewise Function in Matlab This shows that x will take the values from – 5 to + 5. Such a function is said to be defined piecewise. Because this requires two different processes or pieces, the absolute value function is an example of a piecewise function. Now, as the ranges are known we need to declare the total range of input variable ‘ x’. A function may be defined by different formulas on different portions of the x x -axis.
In the above example as we know there are two conditions, therefore, we need to define two ranges. Now we will illustrate the above example by using the vectorize approach, First, we need to declare piecewise function like the above examples.Īfter declaring the piecewise function we will define ranges of input variable ‘ x ’. This is the most popular method in piecewise functions. In this method, the input is the whole vector of sequences(conditions) as well as we can combine two conditions by using ‘ & ’ operator. This method is the second approach of piecewise functions without using loops. The above statements represent ranges of x and respective expected function values. Now inside the switch, there will be different cases, our requirement is only cases so we will write 2 cases. The above statement is the keyword for the switch case for changing values of variable ‘ x’. The above statements show f x is piecewise function concerning input variable ‘ x’, after declaring the function we will start with the switch statement. To implement the above example by using the switch – case statement first, we need to declare the function statement ( piecewise function).
PIECEWISE FUNCTION EXAMPLES PLUS
In this example there are two conditions in function f x, one is less than equal to ‘ 0 ’ and the other one is greater than ‘ 0’. plus an additional P5.00 per mile when the number of miles driven is less than or equal to 100 miles. The example below will contain linear, quadratic and constant pieces. In this method we represent different conditions in different methods, we can specify multiple cases in one switch loop. Due to this diversity, there is no parent function for piecewise defined functions. For example, you are asked to figure out the. The second method in loops is driven by switch-case statements. The floor function or greatest integer function gives the largest integer less than or equal to x. it shows that if the value of x is less than or equal to ‘ 0 ’ then out will be ‘ – 2 ’ and if the value of ‘ x ’ is more than ‘ 0 ’ then the output will be ‘ 2’.

In above statements if-else statement is used to define the range. For example, a piecewise polynomial function is a function that is a polynomial on each of its sub-domains, but possibly a different one on each. In the above statement ‘ f x ’ is the name of the output variable, ‘ piecewise ’ is keyword used for the above function and ‘ x ’ is the input variable.Īfter declaring function now we need to define the conditions of ranges of input variable ‘ x’. To implement the above function in Matlab first we need to create one function with keyword ‘ piecewise ’
Plot ( input variable, output variable )įunction output variable = piecewise ( input variable ) This is one of the basic terminologies to implement piecewise functions but, this is not a good practice to implement piecewise function. The vectorized method By using If-Else statements Continuous functions in the reals need not be bounded or uniformly continuous, but are always piecewise bounded and piecewise uniformly continuous.3.These are infinitely differentiable, but analyticity holds only piecewise. Plot of the piecewise linear function f ( x ) = and some other common Bump functions.


 0 kommentar(er)
0 kommentar(er)
